Introductie tot cryptografie in Java 

Wanneer je aan de slag moet met cryptografie in Java komen er allerlei zaken op je af: Hoe bereik je wat je wil? Welke mechanismen kan je gebruiken? Hoe doe je dat ongeveer? We nemen je mee in dit artikel door een aantal basisbegrippen. Wil je meer weten? Dan zien we je terug in de volgende uitgave van het Java-magazine met do’s and don’ts. 

Door: Nanne Baars & Jeroen Willemsen

Even terug naar wat basisbegrippen 

We komen cryptografie overal tegen in het dagelijks leven: wanneer we een website openen met HTTPS, wanneer we een moderne smartphone aanzetten met versleutelde opslag tot en met wanneer we berichtjes sturen naar onze vrienden/familie met Whatsapp/Signal/Telegram. Maar hoe werkt het nu? En belangrijker: hoe passen we het toe in Java? Voordat we naar de code rennen, laten we eerst even wat basisbegrippen uitleggen die in dit artikel vaak hergebruikt worden. Er zijn 3 security attributen die je graag wil bereiken met cryptografie:

  • Confidentiality: hoe hou je geheimen geheim?
  • Integrity: hoe voorkom je ongeautoriseerde aanpassingen?
  • Non-repudiation: hoe kan je met zekerheid zeggen dat iemand een bericht daadwerkelijk verstuurd heeft?

Cryptografie kent een aantal soorten begrippen:

  • Plaintext: de originele niet versleutelde content. Plaintext hoeft niet per se tekst te zijn: dit kan ook gewoon een serie bytes zijn die bijvoorbeeld bestaat uit gecompileerde applicatiecode.
  • Ciphertext: de tekst waarop een encryptie operatie heeft plaatsgevonden. De inhoud is versleuteld of encrypted.
  • Cipher: een geïnitialiseerd encryptie/decryptie algoritme.
  • Encryption: het versleutelen van plaintext naar ciphertext.
  • Decryption: het ontsleutelen van ciphertext naar plaintext.
  • Signing: het ondertekenen van een bericht
  • Signature: de handtekening als output van een sign operatie.

Nu we de basisbegrippen even wat uitleg hebben gegeven, kunnen we aan de slag. Van bijna alle hieronder genoemde vormen van encryptie hebben we in https://github.com/nbaars/java-magazine-article/ een aantal voorbeelden opgenomen. Deze voorbeelden zijn voorzien van uitgebreid commentaar zodat je deze code kunt hergebruiken. image::images/qr-repo.png[Repo-url,300,200]

Streaming en block-operations 

Voor veel encryptie algoritmes moet de computer allerlei rekenwerk doen op een serie aaneengesloten bits. Vaak is het dan niet efficiënt om deze bits allemaal tegelijk te verwerken. In plaats daarvan is het efficiënter om de serie bits in blokken op te delen van gelijke lengte (bijv. 128 bit) zodat operaties efficiënt uitgevoerd kunnen worden. Op die manier kan je dan iedere keer die 128 bits op dezelfde manier door elkaar halen (transponeren) of als een getal weergeven om er rekenwerk mee te doen. Ciphers die op die manier werken noemen we een “block cipher”.

Daarentegen zijn er ook ciphers die bit-voor-bit kunnen werken. Dit noemen we zogenaamde “stream cipher”. Daarin wordt er vaak per bit een operatie gedaan: bijvoorbeeld een XOR tussen de plaintext bit en een stream aan random bits.

Maar wat nu als we bits overhouden? Stel je voor dat je in blokjes van 128 bits werkt en opeens is het laatste stukje nog te versleutelen plaintext maar 32 bit. Wat doe je dan? Dan moet je de rest van het blokje opvullen, dit noemen we padding.

Symmetrische encryptie 

In het geval dat de encryptie en de decryptie met dezelfde sleutel gebeuren, hebben we het over symmetrische encryptie. Er zijn allerlei block en stream ciphers die dit principe toepassen. Laten we naar twee voorbeelden kijken: Advanced Encryption standard (AES) en ChaCha20.

AES 

AES is één van de bekendste symmetrische encryptie algoritmes. AES beschrijft een encryptie en decryptie algoritme dat een sleutel van 128, 192 of 256 bit neemt en de plaintext encrypt of de ciphertext decrypt. Hoe het precies werkt gaat net even te ver voor dit artikel. Belangrijker is hoe dit algoritme wordt toegepast. Deze verschillende manieren noemen we “modes”. Een aantal bekende modes zijn AES-CBC, AES-GCM en AES-CTR. Laten we eens kijken naar AES-CBC (AES Cipher Block Chaining), in afbeelding 1 zie je een schematische afbeelding.

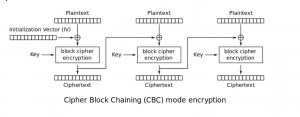
AES CBC (https://en.wikipedia.org/wiki/Block_cipher_mode_of_operation) 

In ieder blok wordt het bericht ge-XOR’ed met de uitkomst uit het vorige blok. Om het eerste blok uniek en onvoorspelbaar te maken, wordt er in het begin geen ciphertext of plaintext gebruikt, maar een block random bits. Dit block noemen we een “Initialization Vector” (IV). Aan het einde van alle operaties kom je bij het laatste blok. Hier moet het blok uiteindelijk ook 128 bit lang zijn. Is de te verwerken plaintext daar korter? Dan komt ook hier de padding om te hoek kijken.

Dit is weer helemaal anders bij AES-CTR (AES-Counter). AES-CTR is een voorbeeld van een stream cipher. Bij een stream cipher wordt er gebruik gemaakt van een keystream die per bit ge-XOR-ed wordt met de plaintext bits bij de encryptie. De keystream wordt verkregen door de block cipher toe te passen op de counter. Doordat er uiteindelijk bit voor bit geXOR-ed wordt, is er geen padding nodig (zie figuur 2). Een voorbeeld van AES-CBC kun je vinden in de Github repository.

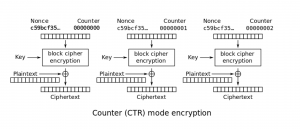
AES CTR (https://en.wikipedia.org/wiki/Block_cipher_mode_of_operation) 

ChaCha20 

Deze stream cipher, beschikbaar in Java 11 1 is ontwikkeld als alternatief op AES. Het voordeel van ChaCha20 is dat deze in de pure software implementatie (dus zonder specifieke hardware AES-ondersteuning) sneller is dan AES. Dit maakt de cipher dus uitermate geschikt in omgevingen zonder krachtige processor. ChaCha20 werkt op basis van 256 bits sleutels en 96 bits nonces, het is een stream cipher wat intern op blocks vertrouwd, net als AES-CTR. Zie ChaCha20 in de Github repository voor een voorbeeld.

Authenticated Encryption with Associated Data (AEAD) 

Bij veel verschillende ciphers heb je nog geen integriteitsbescherming. Bijvoorbeeld bij AES-CBC: indien je een aantal bits in het versleutelde bericht aanpast, kan het best zo zijn dat je nog steeds tot een geldig, maar aangepast bericht kan komen na ontcijfering. Wil je dat vookomen? Dan moeten we de cipher text voorzien van een message authentication code (MAC) waardoor een ontvanger kan detecteren dat het bericht is aangepast. Een veelgebruikte manier is bijvoorbeeld het toepassen AES-CBC met een HMAC, bij ChaCha20 wordt Poly1305 gebruikt hiervoor.

Bij AES-GCM (AES Gallois Counter Mode) zit deze integriteit automatisch ingebakken en hoef je geen extra MAC meer toe te passen. AES-GCM is een voorbeeld van AEAD. Dit staat voor “authenticated encryption” met “associated data”, deze vorm van encryptie biedt naast confidentiality van je bericht ook integriteit en echtheid te controleren. AEAD specificeert een aantal algoritmes waarbij de volgende input wordt verwacht:

  • Key: sleutel voor de encryptie
  • Nonce (number used only once) een getal dat slechts eenmalig gebruikt mag worden onder dezelfde sleutel!
  • Plaintext
  • Associated data wordt niet opgenomen in de ciphertext maar wordt wel meegenomen in de integriteitscontrole, een aanvaller kan dit niet maar zo aanpassen.

Tijdens de ontsleuteling van het bericht wordt allereerst gekeken of de integriteit van het bericht klopt. Is er iets aangepast? Dan stopt het cipher. Is er niets aangepast? Dan wordt het bericht verder ontcijferd.

Als aanvulling kan associated data worden gebruikt om een bepaalde context aan te geven. Bijvoorbeeld: als authenticated associated data kan je een app-identifier gebruiken zodat data alleen te decrypten is op de app-instance met dat app-id.

Let wel op! Een Nonce is géén IV. Een Nonce mag je maar écht 1 keer gebruiken! Gebruik je hem vaker, dan kom je in de problemen. Meer hierover kan je lezen in 2. Aan de andere kant: gebruik echt random IVs als je een IV nodig hebt! Indien je wel een counter gebruikt als IV, dan kan je in de problemen komen. Een voorbeeld hiervan is te vinden in onze Github repository 3.

Uitdaging: maar hoe krijg je de sleutel over de lijn? 

Het grote probleem van symmetrische encryptie is: op welke veilige manier kun je de sleutel delen over een medium zoals het internet? Hier kan asymmetrische encryptie bij helpen.

Asymmetrische encryptie 

Bij deze vorm encryptie hebben de verzender (voor nu even Alice) en de ontvanger (noemen we Bob) allebei 2 sleutels: 1 publieke sleutel en een geheime privésleutel. Deze sleutels vormen een keypair. De publieke sleutel kunnen Alice en Bob met elkaar delen. Als Alice een bericht naar Bob wil sturen gebruikt Alice de publieke sleutel van Bob en versleutelt hiermee het bericht. Vanaf dat moment is Bob de enige die het bericht kan ontcijferen omdat Bob de privé sleutel heeft.

Hoe de sleutel uitwisseling in de praktijk op een veilige manier moet gebeuren is buiten de scope van dit artikel. Je kan je voorstellen dat ook hier van alles mis kan gaan. Stel je voor dat Alice haar publieke sleutel naar Bob wil sturen en een derde partij (voor nu even Mallory) het bericht onderschept. Mallory geeft dan haar publieke sleutel in plaats van die van Alice aan Bob. Als Bob dan een sleutel wil uitwisselen met Alice, gebruikt hij de publieke sleutel van Mallory, die vanaf dan dus met de conversatie kan meeluisteren omdat ze de bijbehorende private sleutel heeft.

Hoe de sleutel uitwisseling in de praktijk op een veilige manier moet gebeuren is buiten de scope van dit artikel. Want ook hier kan van alles misgaan.

Voor nu hebben we twee voorbeelden van asymetrische cryptografie: RSA (Ron Rivest, Adi Shamir, and Len Adleman) en ECC (Elliptic Curve Cryptography):

RSA & ECC 

RSA is ontwikkeld in 1978 en gebruikt priemgetallen en vermenigvuldigingen mod N. Het principe is gebaseerd op het feit dat het ontbinden van priemgetallen een moeilijk probleem is. Het vinden van de juiste grote priemgetallen wordt gelukkig door Java voor je opgelost, zodat je uiteindelijk tot een publieke exponent en de juiste publieke N komt als publieke sleutel. RSA-X staat ook eigenlijk voor de lengte van N in bits: bij RSA-1024 is N 1024 bits lang, bij RSA-4096 is N 4096 bits lang.

ECC maakt gebruik van elliptische krommen over eindige velden en discrete logaritmes wat net zoals bij RSA een moeilijk probleem is. Deze krommen zijn vastgesteld en worden gevalideerd 4. Eén van de voordelen van ECC is dat de grootte van de sleutel kleiner is, maar wel sterker. Dit maakt ECC efficiënter en beter te gebruiken in het geval van beperkte rekenkracht. Het aantal valkuilen bij het vinden van een curve is ook groter, in het tweede artikel zullen we hier meer aandacht aan besteden.

Praktijk 

Met een asymmetrisch cipher kun je per keer slechts een beperkt aantal bits versleutelen bijvoorbeeld met RSA-2048 kan het bericht uit maximaal 2048 bits bestaan (minus de padding). Bij ECC wordt de grootte bepaald door het veld van de curve. Hoe wordt dit nu gebruikt? Wanneer je sleutels uitwisselt kan je RSA of EC gebruiken om de symmetrische sleutel te versleutelen om deze uit te wisselen. Een voorbeeld hiervan is Elliptic-curve Diffie–Hellman (ECDH), dit is een ‘key agreement protocol’ waarbij de symmetrische sleutel over een onveilig medium toch uitgewisseld kan worden. Deze symmetrische sleutel wordt dan gebruikt om het bericht vervolgens te versleutelen.

Hashing 

Stel je voor: je verstuurt een bericht via een onbetrouwbaar medium, hoe kan je dan een indicatie krijgen of deze niet is aangetast onderweg? In andere woorden: hoe krijg je een indicatie van de integriteit van een bericht? In onze Github repository 5 kan je het voorbeeld ChangeCipher vinden. Hierin is te zien hoe je een bericht kan aanpassen als attacker. Wil je de integriteit kunnen controleren? Dan kan dit onder andere door het gebruik van een hashing methode. In feite wordt er over een plaintext met een hashfunctie een hash berekend: H(Plaintext) = hash. De plaintext kan oneindig lang zijn, terwijl de hash altijd een vaste lengte heeft. Je voelt hem wel aankomen: als iedere plaintext in de wereld door de hash functie heen tot een hash komt met een vaste lengte, dan heb je dus ergens wel 2 berichten die allebei dezelfde hash hebben. Dit noemen we een collision. Om te voorkomen dat je collisions krijgt, moet je een hash-algoritme kiezen dat een zo hoog mogelijke collision resistance heeft. De SHA (Secure Hash Algorithm) familie is een groep aan hashes die een steeds hogere collision resistance heeft. Op dit moment kunnen we dan ook aanbevelen om SHA-2 (256 bits of hoger) of SHA-3 (256) te gebruiken.

Ondertekenen van een bericht 

Waar je met een hash vooral keek of de integriteit in orde was, ga je met een signature een stap verder: je valideert de integriteit van een bericht en je controleert of het bericht ook op die manier is verstuurd door de afzender. Een signature wordt namelijk gemaakt door een private key die alleen de verstuurder heeft. Je kan de signature dan weer valideren met de public key. Signatures zijn operaties die je niet op grote blokken plaintext direct kan zetten. In plaats daarvan wordt de hash van een bericht ondertekend. De ondertekening daarvan controleer je vervolgens door met de public key te valideren dat de signature klopt. Hoe gaat dit in zijn werk? Bekijk de onderstaande code:

public static byte[] signRsaPssSha512(byte[] privateKey, byte[] msg) {
PSSSigner signer = new PSSSigner(new RSAEngine(), new SHA512Digest(), new SHA512Digest(), new SHA512Digest().getDigestSize());

try {
RSAPrivateCrtKeyParameters key = (RSAPrivateCrtKeyParameters) PrivateKeyFactory.createKey(privateKey);
signer.init(true, key); //true means: sign
signer.update(msg, 0, msg.length);
return signer.generateSignature();
} catch (IOException | CryptoException e) {
throw new IllegalStateException(e);
}
}

De plaintext msg in de code wordt hier ondertekend. Om dit te doen wordt er eerst een PSSSigner klasse in het leven geroepen die een hashfunctie meekrijgt om een hash over het bericht te berekenen. De andere kant kan met de publieke sleutel de signature valideren.

We hebben nu alle bouwblokken beschreven en in het volgende artikel zullen we een aantal constructies uitlichten waar je op moet letten als je encryptie gaat gebruiken in productiecode.